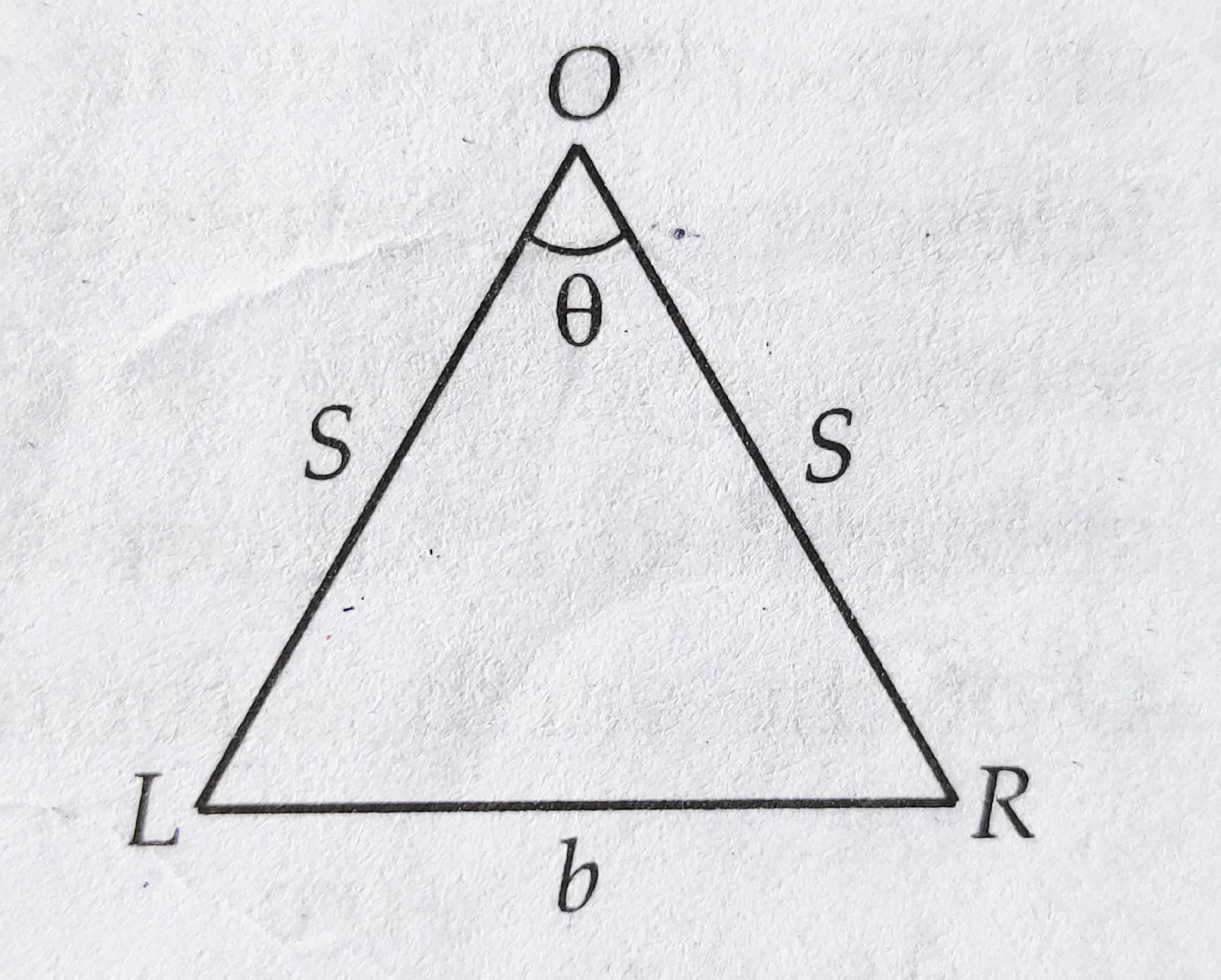CLASS XI | PHYSICS | CHAPTER 2 notes prepared by subhankar Karmakar
PHYSICAL QUANTITIES:
All those quantities which can be measured directly or indirectly and in terms of which the laws of Physics can be expressed are called physical quantities. For example, length, mass, time, speed, temperature, force, electric current, angle etc are physical quantities.
TYPES OF PHYSICAL QUANTITIES:
Physical quantities are of two types:
a. Fundamental quantities
b. Derived quantities
a. FUNDAMENTAL QUANTITIES:
The physical quantities which can be treated as independent of other physical quantities and are not usually defined in terms of other physical quantities are call fundamental quantities. There are seven fundamental quantities, and two supplementary fundamental quantities.
The fundamental or base quantities are:
1. Mass
2. Length
3. Time
4. Electric current
5. Thermodynamic temperature
6. Luminous intensity
7. Amount of substance
Two supplementary fundamental quantities are:
1. Angle
2. Solid angle
b. DERIVED QUANTITIES:
The physical quantities who's defining operations are based on other physical quantities are called derived quantities. All physical quantities other than fundamental quantities are derived quantities. For example, velocity, speed, acceleration, force, momentum etc are derived quantities.
THE MEASURING PROCESS:
Measurement: The measurement of a physical quantity is the process of comparing this quantity with a standard amount of the physical quantity of the same kind, called its unit.
The measurement of a physical quantity has two components.
1. The unit in which the quantity is measured (u)
2. The numerical value or the magnitude of the quantity. (n)
If the measure of a physical quantity = Q
Numerical value of the physical quantity = n
Size of the unit = u, then
Q = nu
If n₁ and n₂ are the numerical values for a physical quantity Q corresponding to the units u₁ and u₂ , then
Q = n₁u₁ = n₂ u₂
PHYSICAL UNIT:
The standard amount of a physical quantity chosen to measure the physical quantity of the same kind is called a physical unit.
Desirable characteristics of a physical unit:
1. It should be well defined.
2. It should be of convenient size. Neither too small, nor too large.
3. It should not change with time.
4. It should be easily reproducible.
5. It should be imperishable or indestructible.
6. It should not be affected by the change in physical conditions such as variation of pressure temperature etc.
7. It should be internationally acceptable.
8. It should be easily accessible.
FUNDAMENTAL & DERIVED UNITS:
Fundamental units: The physical units which can neither be derived from one another, nor they can be further resolved into more simpler units are called fundamental units. Units of fundamental quantities are fundamental units.
Derived units: All the other physical units which can be expressed in terms of the fundamental units are call derived units. Like unit of force is Newton, but it can be expressed in terms of fundamental units.
Force = Mass x acceleration
1 N = 1 kg x 1 m /s² = 1 kg m /s²
DIFFERENT SYSTEM OF UNITS:
a. cgs system = It was set up in France. It is based on centimetre, gram and second as the fundamental units of length, mass and time respectively.
b. mks system = It is also a French system based on metre, kilogram and second as the fundamental units of length, mass and time respectively.
c. SI system = It is the international system of units. What is the modernization extended form of the mks system.
BASIC SI QUANTITIES AND UNITS:
Basic quantity - basic unit - symbol
1. Length - metre - m
2. Mass - kilogram - kg
3. Time - second - s
4. Temperature - kelvin - K
5. Electric Current - ampere - A
6. Luminous Intensity - candela - cd
7. Quantity of matter - mole - mol
Supplementary units
1. Angle - radian - rad
2. Solid angle - steradian - sr
Definition of Radian and Steradian:
1. Radian: it is defined as the plane angle subtended at the centre of a circle by an Arc equal in length to the radius of the circle.
θ (in radians) = arc/radius = l/r
2. Steradian: it is defined as the solid angle subtended at the centre of a sphere why the surface of the sphere equal in area to that of a square having each side equal to the radius of the sphere.
Ω (in steradian) = surface area/ radius²
Some common practical units:
1. Fermi = it is also known as femtometre. It is a very small unit of distance. It is used to measure nuclear distance. The radius of a proton is 1.2 fermi.
1 fermi = 10⁻¹⁵ m
2. Angstrom (Å):
It is also a small unit of distance. It is used express wavelength of light.
1 Å = 10⁻¹⁰ m = 10⁻⁸ cm
3. Nano-metre:
It is also used to express wavelength of light.
1 nano metre = 10⁻⁹ m
4. Micron (μm)
It is also known as micro metre.
1 μm = 10⁻⁶ m
5. Astronomical Unit ( AU)
It is defined as the the mean distance of the earth from the sun. It is a practical unit used for measuring large distances. It is used in astronomy to measure distances of planets.
1 AU = 1.496 x 10¹¹ m
6. Light year (ly)
It is the distance travelled by light in vacuum in one year. Light year is used in astronomy to measure distances of nearby stars. Like alpha centauri, the nearest are outside the solar system is 4.3 light years away from the Earth.
1 ly = 9.467 x 10¹⁵ m
7. Parsec or Parallactic Second:
It is the largest practical unit of distance used in astronomy. It is defined as the distance, at which an Arc of length 1 astronomical unit subtends an angle of 1 second of arc.
1 parsec = 3.26 ly = 3.08 x 10¹⁶ m
Indirect method for measuring large distances:
a. Triangulation method for the height of an inaccessible object.
b. Parallax method to measure the distance of a nearby star.
* Sextant: sextant is an instrument by which we can measure the angle of a distant object with the horizontal.
a. Triangulation method for the height of an inaccessible object.
Let AB = h be the height of the mountain to be measured. By using a sextant, we first measure the angle of elevation of its peak from my point C on the ground. Let it be
θ₁ or ∠ACB =
θ₁ . Move the sextant to another position D such that CD = d. Again measure the angle of elevation, ∠ADB =
θ₂ . in right triangle ∆ABC,
cot θ₁ = CB/AB = x /h
in right triangle ∆ABD,
cot θ₂ = DB/AB = (d + x )/h
cot θ₂ - cot θ₁ = (d + x )/h - x/h = d/h
∴ h = d / ( cot θ₂ - cot θ₁ )
Hence, if we know d , the height h can be determined.
b. Parallax method
Parallax: parallax is the apparent shift in the position of an object with respect to another when we shift our eye side wise.
suppose we hold a pen O at a distance S from the eyes. Look at the pen first by the left eye L closing the right eye, and then buy the right eye R closing the left eye. The position of the pen appears to change with respect to the background. This is called
parallax. The distance between the two points of observation is called basis. In this case, the distance LR = b between the two eyes is the basis.
∠LOR = θ is called
parallax angle or
parallactic angle.
Parallax method can be used to find the
1. Distance of moon or any other planet.
2. Distance of a nearby star.
1. Distance of moon or any other planet.
To measure the distance S of the moon or a faraway planet P, we observe it simultaneously from two different positions (observatories) A and B on the earth, separated by a large distance AB = b. We select a distant star S' whose position and direction can be taken approximately same from A and B.
Now, ∠PAS' = Φ₁ and ∠PBS' = Φ₂ are measured from the two observatories at the same time. As b<<S, so we can take AB as an arc of length b.
Now θ = Arc/Radius = b/s
∴ S = b/θ
where θ = ∠APB = Φ₁ + Φ₂ , is the parallactic angle.
2. Distance of a nearby star.
Suppose N is a nearby star whose distance d from the earth is to be found. F is a far off star whose direction and position is fixed for all the position of the earth in its orbital motion. When the earth is at position A, the parallax angle between distance star F and nearby star N is determined. Let it be θ₁ . After 6 months, the earth is at diametrically opposite position B. The parallax angle
∠NBF = θ₂ is measured.
Total parallax angle subtended by N on the earth's orbital diameter AB is
θ = θ₁ + θ₂
As, θ = Arc/Radius
θ = AB/d
∴ d = AB/θ
This Parallax method is useful for measuring distances of stars which are less than 100 light years away from the Earth.